Wer ist der Klassenprimus? Unser Predictive Analytics Cube (PAC) macht Prognosemodelle vergleichbar
Das Problem (vergleichbarer) Prognosen
In den letzten Jahren hat sich die Prognose von Zeitreihen zu einem Bereich innerhalb der Data Science entwickelt, in dem sich etablierte statistische und ökonometrische Methoden mit modernen Machine Learning-Techniken vermischen. Solide Standards für die Datenpartitionierung oder vergleichbare Modellevaluation haben sich jedoch noch nicht durchgesetzt.
Prognosen sind ein zentraler Bestandteil unserer Arbeit bei INWT. Wir nutzen sie für eine breite Palette von Anwendungen, darunter Umsatzprognosen, Personalplanung und Luftqualitätsüberwachung. Wenn in unseren Timelines die Ankündigung eines neuen, angeblich revolutionär guten Prognosemodells auftaucht, stehen wir vor der Herausforderung, die Spreu vom Weizen zu trennen: Hält dieses Modell wirklich, was es verspricht? Oder genauer gesagt, hält es sein Versprechen, wenn es in einer kontrollierten Umgebung auf von uns gewählten Daten praktisch angewendet wird? Was genau sind die Stärken und Schwächen dieses speziellen Prognosemodells? Um diese Fragen zu beantworten, haben wir beschlossen, unseren eigenen Predictive Analytics Cube (PAC) zu bauen.
Der Zweck unseres PACs ist es, eine Infrastruktur von Daten, Modellen, Prognosen und Berichten aufzubauen, die auf Grundlage einer standardisierten Bewertung einen schnellen Vergleich von Modellen hinsichtlich ihrer Vorhersagekraft ermöglicht. Unser PAC soll uns dabei helfen, bei einem bestimmten Vorhersageproblem schnelle und besser informierte Entscheidungen zur Auswahl der Modellklasse zu treffen. Welches Modell ist zum Beispiel für eine niedrigfrequente Zeitreihe mit starker Saisonalität und starkem Trend am vielversprechendsten? Und wenn eine neue Modellklasse die mittlerweile riesige Arena verschiedenster Methoden für Prognosen betritt: Wie gut schneidet sie bei einem bekannten Datensatz ab, und wie schneidet sie im Vergleich zu anderen Modellen ab? Wir möchten, dass unser PAC uns eine nachvollziehbare und differenzierte Antwort auf die Frage "Welches Modell ist das Beste?" gibt. Und wenn die Antwort dabei nicht eindeutig oder verallgemeinerbar ausfällt, geht das in Ordnung - schließlich suchen wir immer nur nach der besten Lösung für ein bestimmtes Prognoseproblem.
Wir haben uns entschlossen unseren eigenen PAC zu bauen, um eine auf unsere Ziele und Anforderungen bei INWT zugeschnittene Lösung zu haben - und schließlich unseren Kund*innen qualitativ hochwertige, moderne Lösungen anbieten zu können. Wir wollen in der Lage sein, den PAC selbst und mit wenig Aufwand um neue Modelle und Daten zu erweitern. Daher wollten wir ähnliche Projekte wie das beeindruckende Monash Time Series Forecasting Repository oder das innovative Out-of-sample time series forecasting Paket nicht forken, sondern diese Projekte als Inspiration und Kompass für unser eigenes Projekt nutzen.
Aufbau unseres PACs
Unsere erste, minimale Version des PACs enthält vier Modelle und drei univariate Zeitreihen. Derzeit beschränken wir den PAC auf univariate Prognosen und zukünftige Werte werden ausschließlich anhand der vergangenen Werte einer Zeitreihe prognostiziert. Schauen wir mal unter die Haube des PACs, um zu sehen, wie wir Daten, Methoden und Evaluation miteinander verwoben haben.
Architektur
Das Rückgrat unseres PACs bilden zwei R-Pakete, die wir entwickelt haben. PacModel fragt die Trainingsdaten aus einer MariaDB-Datenbank ab und übergibt sie an die Modelle. Die Modelle laufen auf den Trainingsdaten und senden ihre Prognosen in-sample und out-of-sample zurück an die Datenbank. PacReport fragt dann diese Prognosen ab und erstellt einen umfangreichen html-Bericht über rmarkdown.
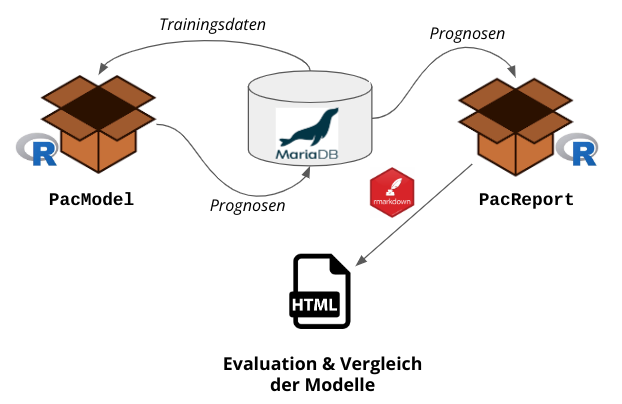 Aktuelle Architektur des PACs
Aktuelle Architektur des PACs
Datensätze
| Zeitreihen | Info | Beobachtungen (Frequenz) | Quelle |
| Reales Bruttoinlandsprodukt (BIP) von Deutschland in preisbereinigten Millionen Euro (Basisjahr 2010) | Keine Saisonalitätsanpassung 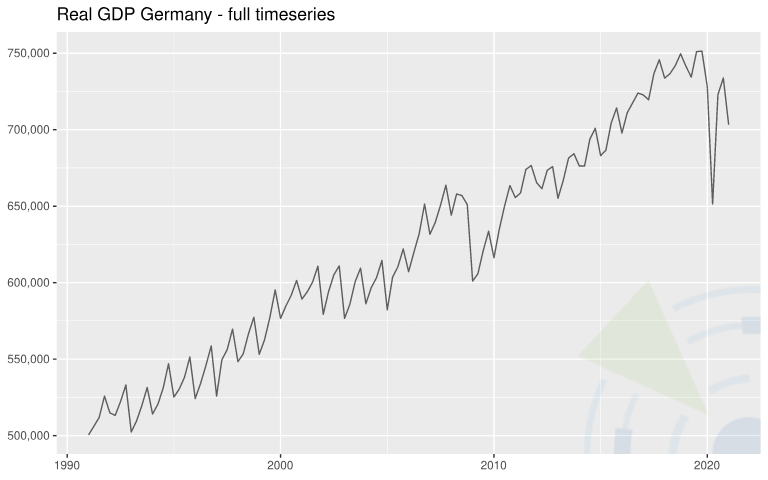 | 121 (quartalsweise) | Eurostat, Real Gross Domestic Product for Germany [CLVMNACNSAB1GQDE], runtergeladen von der FRED, Federal Reserve Bank of St. Louis. |
| Elektrizitätsnachfrage im Bundesstaat New South Wales (NSW) Australien | Die Daten wurden auf täglicher Ebene aggregiert. 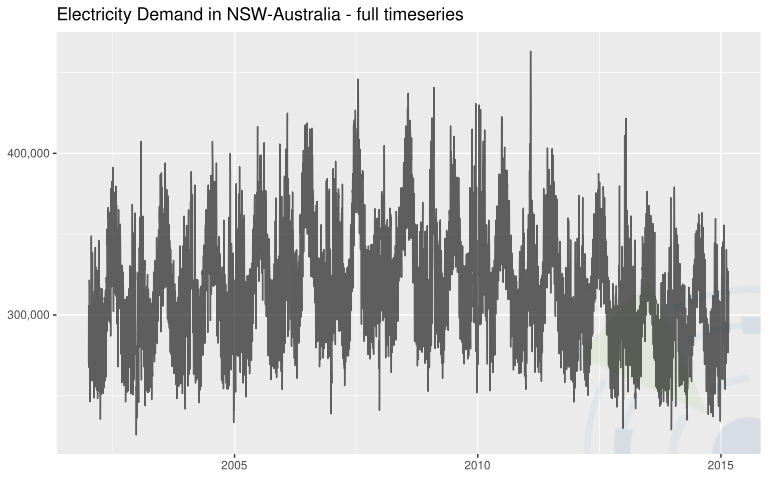 | 4807 (täglich) | Godahewa, Rakshitha, Bergmeir, Christoph, Webb, Geoff, Hyndman, Rob, & Montero-Manso, Pablo. (2021). Australian Electricity Demand Dataset (Version 1) [Data set]. Zenodo. |
| Solarenergieproduktion in Megawatt (MW) in Australien | Die Daten wurden auf täglicher Ebene aggregiert, um die Nullwerte in der Nacht zu entfernen. 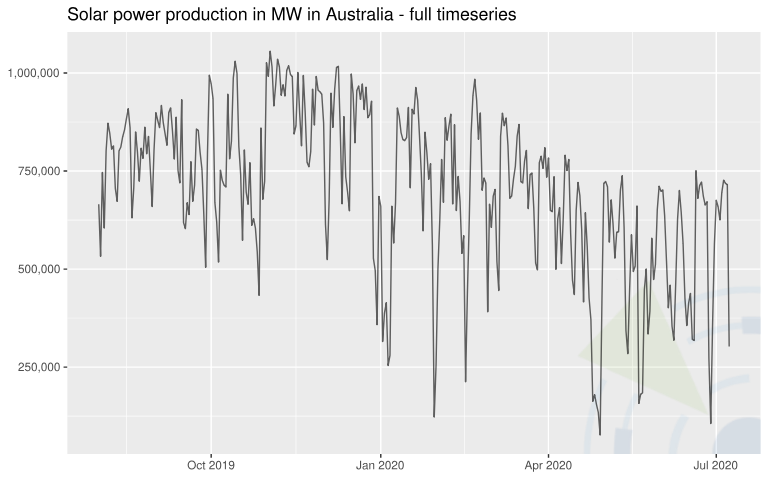 | 343 (täglich) | Godahewa, Rakshitha, Bergmeir, Christoph, Webb, Geoff, Abolghasemi, Mahdi, Hyndman, Rob, & Montero-Manso, Pablo. (2020). Solar Power Dataset (4 Sekunden Beobachtungen) (Version 2) [Data set]. Zenodo. |
Modelle
| Modell | R Paket::Funktion | Info |
| ARIMA | forecast::auto.arima() | Die Funktion verwendet eine Variation des Hyndman-Khandakar-Algorithmus, der Unit-Root Tests, Minimierung des AICs und MLEs kombiniert, um ein (saisonales) ARIMA-Modell zu erhalten. |
| ARIMA W/ XGBOOST ERRORS | forecast::auto.arima() and xgboost::xgb.train() | Wie das vorherige ARIMA-Modell, nur mit zusätzlichem Boosting zur Verbesserung der Residuenstruktur bei exogenen Prädiktoren.. |
| ETS | forecast::ets() | Ein Exponential Smoothing State Space Modell, das ARIMA-Modellen insofern ähnelt, als dass eine Vorhersage eine gewichtete Summe vergangener Beobachtungen repräsentiert. Das Modell verwendet aber eine exponentiell abnehmende Gewichtung für vergangene Beobachtungen. Ein möglicher Trend oder eine Saisonalität werden automatisch geschätzt, ebenso wie der Fehler, der Trend und der Saisonalitätstyp. |
| PROPHET | prophet::prophet() | Prophet wurde von Facebook entwickelt und basiert auf einem additiven Modell, bei dem nichtlineare Trends mit jährlicher, wöchentlicher und täglicher Saisonalität sowie Urlaubseffekten angepasst werden. Potenzielle changepoints werden automatisch ausgewählt. |
Evaluation
Wir bewerten unsere Modelle in erster Linie auf der Grundlage ihrer out-of-sample (oos) Performance. Um die Daten in Trainings- und Testdaten aufzuteilen, wählten wir ein Rolling-Origin-Setup, bei dem "die Größe des Prognosehorizonts fix bleibt, aber der Prognoseursprung entlang der Zeitreihe immer weiter ‘rollt’ [...], wodurch effektiv mehrere Testperioden für die Bewertung geschaffen werden." (Hewamalage et al. 2022) Außerdem haben wir uns dazu entschlossen, das Fenster der Trainingsdaten bei jedem Modelldurchlauf um einen weiteren Datenpunkt zu vergrößern. Dieser Ansatz eines expandierenden Trainingsdatenfensters wird auch als time series cross-validation (tsCV) bezeichnet (Hyndman, R.J., Athanasopoulos, G., 2021) - eine Art der Kreuzvalidierung, welche die zeitliche Ordnung der Daten erhält. Im Moment beschränken wir uns auf one-step-ahead Prognosen, möchten aber in Zukunft flexible Prognosehorizonte implementieren.
 Visualisierung des expandierenden Trainingsdatenfensters, verbunden mit einem je Modelldurchlauf um einen Datenpunkt weiter “rollenden” Prognoseursprung. Die blauen Punkte stehen für die Datenpunkte der Trainingsdaten. Die roten Punkte hingegen stehen für die Datenpunkte der Testdaten und dienen der oos Evaluation. Quelle: Hewamalage et al. 2022.
Visualisierung des expandierenden Trainingsdatenfensters, verbunden mit einem je Modelldurchlauf um einen Datenpunkt weiter “rollenden” Prognoseursprung. Die blauen Punkte stehen für die Datenpunkte der Trainingsdaten. Die roten Punkte hingegen stehen für die Datenpunkte der Testdaten und dienen der oos Evaluation. Quelle: Hewamalage et al. 2022.
Um potenzielle Overfitting Probleme zu erkennen, messen wir zusätzlich die in-sample Performance jedes Modells auf jedem Datensatz. Zu diesem Zweck erstellen wir für jeden Datensatz einen Snapshot des ersten (=kleinsten) und des letzten (=größten) Trainingsdatenfensters und bewerten die Prognosen für diese Datenpunkte. Insgesamt bietet uns die rollierende oos-Struktur mit expandierendem Trainingsdatenfenster gemeinsam mit der Overfitting Überwachung ein realistisches Setup, das unseren üblichen Business Cases entspricht: Die verfügbaren Daten nehmen mit der Zeit zu, während eine häufige Rekalibrierung des Modells für optimale Prognosen sowohl möglich als auch wünschenswert ist.
Um einfache Vergleichbarkeit der Performance verschiedener Modelle zu erreichen, haben wir beschlossen, ein Modell als Baseline für alle Datensätze festzulegen und entschieden uns für ein Exponential Smoothing State Space (ETS) Modell. Dieses Modell liefert ziemlich gute Prognosen auf Grundlage einer Faustregel für Zeitreihenglättung. Das von uns verwendete Modell erfordert kein Finetuning, da es vollautomatisiert ist. Es berücksichtigt einen potenziellen Trend oder potentielle Saisonalität und wählt den Fehler-, Trend- und Saisonalitätstyp bequemerweise auch automatisch aus (entweder additiv oder multiplikativ). Wir haben das ETS-Modell aufgrund seiner relativen Einfachheit und seiner guten "out of the box" Performance als unsere Baseline gewählt.
Um die Prognosegüte unserer verschiedenen PAC-Modelle zu beurteilen, verwenden wir in erster Linie relative Gütemaße, d.h. Verhältnisse eines Fehlermaßes für das Prognosemodell geteilt durch das unseres ETS-Benchmark-Modells. Geeignete relative Gütemaße sind zum Beispiel der Relative Mean Absolute Error (RelMae) oder der Relative Root Mean Squared Error (RelRMSE). Diese relativen Gütemaße sind sehr hilfreich, weil sie leicht zu interpretieren sind (Werte < 1 stehen für eine Performance besser als die des Baseline Modells, Werte > 1 für eine schlechtere Performance) und immer bequem durch den Benchmark-Fehler des Baseline Modells für jede Zeitreihe individuell skaliert werden. Mit anderen Worten: Für einen bestimmten Datensatz liefern relative Gütemaße Statistiken zur Performance eines Modells, die über alle Arten von Modellen hinweg vergleichbar sind. Wir sind uns der Probleme bewusst, die relative Gütemaße verursachen können - z.B. bei Zeitreihen mit Trend oder Unit Root (Hewamalage et al. 2022, S. 44 ff.). Glücklicherweise werden diese Probleme erst bei längeren Prognosehorizonten richtig relevant, die wir zu diesem Zeitpunkt gar nicht verwenden. Wir haben daher beschlossen, die Bearbeitung dieser speziellen Probleme der Modellevaluation zu verschieben, bis wir unseren PAC auf längere Prognosehorizonte erweitern. Aber natürlich ist uns auch bewusst, dass die tiefgehende Bewertung eines bestimmten Modells unseres PACs die Verwendung diverser Gütemaße erfordert, und die Betrachtung relativer Gütemaße allein nicht ausreicht.
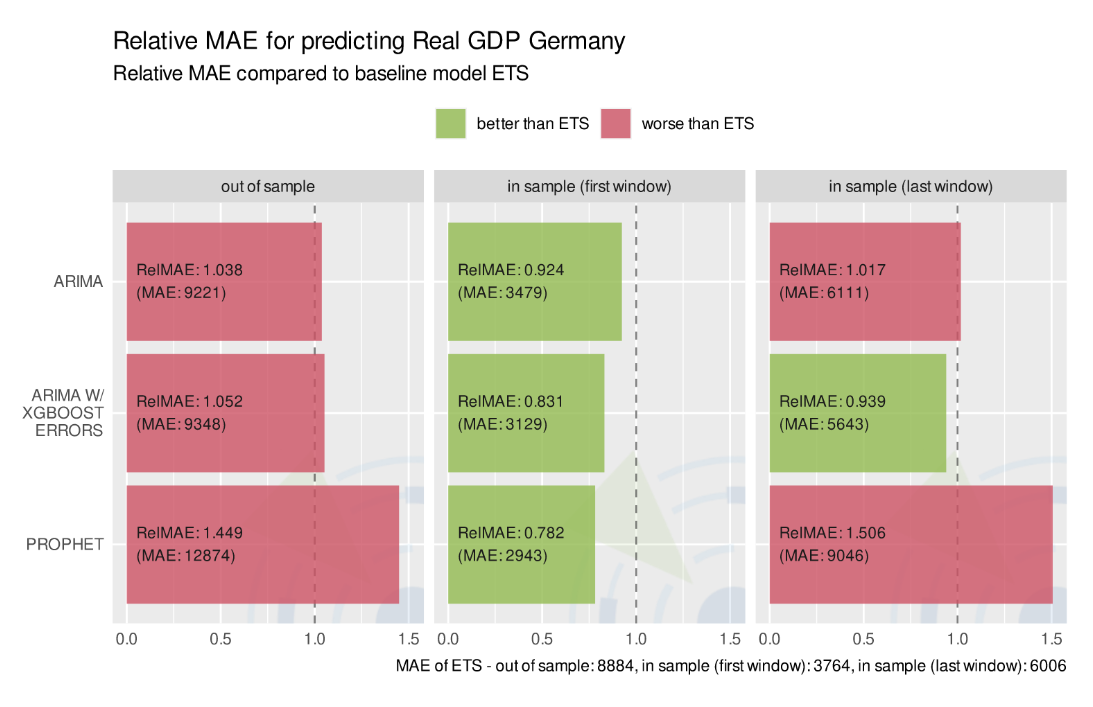 Modellperformance für die Prognose des realen Bruttoinlandsproduktes von Deutschland, gemessen am Relative Mean Absolute Error.
Modellperformance für die Prognose des realen Bruttoinlandsproduktes von Deutschland, gemessen am Relative Mean Absolute Error.
Lessons learned und Zukunftspläne
Unser PAC befindet sich noch in einer Frühphase, man kann ihn als Minimal Viable Product (MVP) ansehen. Dennoch bietet der PAC bereits einen leicht erweiterbaren Rahmen für den Vergleich von Prognosemodellen auf verschiedenen Datensätzen. Schon das Erreichen dieses MVP Stands war mit einigen Herausforderungen verbunden. Eine Herausforderung, die wir sicherlich unterschätzt haben, ist der Trade Off zwischen Automatisierung und Tuning. Einerseits wollen wir sehen, wie ein Modell "out of the box" mit so wenig Konfiguration wie möglich funktioniert, wenn es mit verschiedenen Datenszenarien konfrontiert wird. Andererseits würden wir ein Modell nicht "fair" behandeln, wenn wir es wissentlich mit zu wenig Konfiguration in die Prognose schicken. Tatsächlich ist es für uns kein realistisches Geschäftsszenario, ein Modell mit sehr wenig Konfiguration und Tuning in Produktion einzusetzen. Modelle werden vor ihrem Einsatz genau eingestellt. Trotzdem erwarten wir, dass unser PAC uns bereits im Vorfeld einen realistischen Hinweis auf die Prognosefähigkeit eines Modells liefert.
Ein weiterer schwieriger Diskussionspunkt bei der Entwicklung unseres PACs war es, ein sinnvolles Baseline Modell zu finden, das für verschiedene Zeitreihen geeignet ist. Diese Wahl ist nicht trivial, wenn das Modell einigermaßen naiv und flexibel sein soll, um gleichzeitig mit Saisonalität, Trend und Unit Roots umgehen zu können. Von unseren initialen vier PAC-Modellen schien das ETS das Naivste zu sein, aber dennoch flexibel genug, um sich als Baseline zu qualifizieren. Nach einer langen Diskussion haben wir uns daher für das ETS als Baseline entschieden, wohl wissend, dass wir eventuell unsere Entscheidung später revidieren müssen, wenn der PAC wächst.
Unsere ToDo Liste ist voller Ideen, wie wir unseren PAC nun erweitern und verbessern wollen. Hier sind einige mögliche Erweiterungen, die wir derzeit in Betracht ziehen:
- Einbeziehung exogener, zeitvariabler Prädiktoren, welche die Zeitreihen beeinflussen können,
- Flexibilisierung der Prognosehorizonte, um Vorhersagen mit n-steps-ahead zu ermöglichen,
- Integration von Python-Modellen in unsere von R-Paketen gestützte PAC Architektur,
- eine CI/CD-Automatisierung mit Hilfe von Jenkins einzuführen, die, sobald ein neues Modell oder ein neuer Datensatz zum PAC hinzugefügt wird, neue Modellschätzungen und -evaluationen durchführt,
- unseren standardisierten html-Bericht in ein vue.js-Dashboard zu überführen,
- neue Modelle und Datensätze hinzuzufügen.
Dies ist erst der Anfang unseres PACs. Weitere Blogposts mit detaillierten Analysen einzelner Modelle und andere Einblicke in Weiterentwicklungen der Methodik und Automatisierung unseres PACs werden folgen…